Построение оптимального плана поставок сырья для предприятия ООО «Ресурс»

Построим оптимальный план поставок сырья для предприятия ООО «Ресурс». В день комбинат может переработать 3,15 тонн продукции. Плата за хранение 1 тонны продукции составляет 1685 рублей. Затраты на доставку составляют 2102 рубля. Найдем оптимальный план поставок на 2010 год отдельно для каждого месяца.

Горизонт планирования на первый месяц T=31 день. По формуле (3) рассчитываем

Множество допустимых значений для Q имеет вид

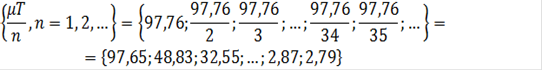
Следовательно, Q1 = 2,79 и Q2 = 2,87. Первое значение определяет напряженный план с тридцатью пятью одинаковыми зубцами, а второе - с тридцатью четырьмя. Поскольку

то

и

Поскольку f1(Q1) < f1(Q2), то Qопт = Q1 = 2,79. Итак, оптимальным является напряженный план с тридцатью пятью зубцами.

Как уже отмечалось, часто рекомендуют применять план поставок с Q=Q0. Каков при этом проигрыш по сравнению с оптимальным планом?

Для плана с Q=Q0 интервал между поставками составляет дня. Следовательно, партии придут в моменты t0 = 0; t1= 0,89; …; t34 = 30,23; t35 = 31,15. Следующая партия должна была бы прийти уже за пределами горизонта планирования Т =31, в момент t35 = 31,15. Таким образом, график уровня запаса на предприятии в пределах горизонта планирования состоит из тридцати четырех полных зубцов и одного не полного. К моменту Т =31 пройдет 31 - 30,23 = 0,77 дня с момента последней поставки, значит, комбинат переработает 2,43 т продукции и останется 0,375 тонны. План с Q=Q0 не является напряженным, а потому не является оптимальным для горизонта планирования Т =31. Но так как горизонт планирования достаточно велик и разница между моментом последней поставки и горизонтом планирования составляет всего 0,15 дня, то будем считать оптимальным план с Q=Q0.

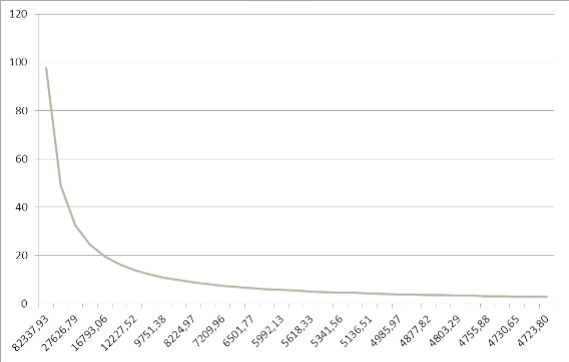
Рисунок 1.3. График зависимости средних издержек от оптимального объема партии

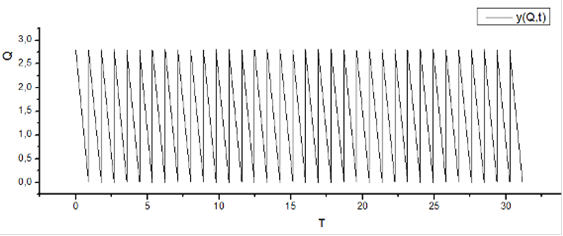
Рисунок 1.4. График оптимального плана

Подсчитаем общие издержки в плане с Q=Q0. Площадь под графиком уровня запаса на складе равна сумме площадей тридцати четырех треугольников и трапеции. Площадь треугольника равна 1,246, а тридцати четырех - 42,364. Основания трапеции параллельны оси ординат и равны значениям уровня запаса в моменты времени t34 = 30,23 и Т =31, т.е. величинам 2,8 и 2,43 соответственно. Высота трапеции лежит на оси абсцисс и равна 31 - 30,23 = 0,77, а потому площадь трапеции есть . Следовательно, площадь под графиком равна 42, 364 + 2,014 = 44,378, а плата за хранение составляет рублей.

За 31 дней доставлены 35 партий сырья , следовательно, затраты на доставку равны рублей. Общие издержки за 31 дней составляют + = 148346,17 рублей, а средние издержки - 4785,36 рублей. Они больше средних издержек в оптимальном плане в 4785,36/4723,801 = 1,013 раза, т.е. на 1,3%.

Отметим, что

т.е. меньше, чем в плане с Q=Q1. Таким образом, из-за дискретности множества допустимых значений средние издержки возросли на 0,56 рубля. При этом оптимальный размер партии (3,79 т) отличается от Q0 = 2,8 т на 0,01 тонну, т.е. Qопт/ Q0 = 0,996 - различие на 0,4%. Таким образом отличие плана с Q=Q0 от оптимального пренебрежительно мало на достаточно большой горизонт планирования.

Оба слагаемых в f1(Q0) почти равны между собой

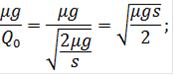
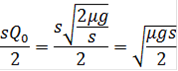
Таким образом, составляющие средних издержек, порожденные различными причинами, уравниваются между собой.

Средние издержки в плане с Q=Q0 равны . Интервал между поставками при этом равен