Быстрое преобразование Фурье длины 5

Для коэффициентов при, согласно (10) - (12)

,

,

,

,

,

,

,

Если произведение вычисляется в кольце F(так что ), то формулы (10) - (12) принимают вид:

≜, (10а)

, ≜

,

.

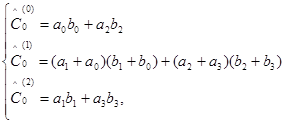
Вычисление вектора гдеа - циркулянт, первая строка которого задается вектором , равносильно вычислению в F произведения , где

и .

Подчеркнем, что преобразуемая последовательность , за исключением первого элемента, дает реверсивный порядок коэффициентов многочлена при координате стоит коэффициент .

Утверждение 4.5.2.

Для ДПФ простой длины n всегда существует такая перестановка строк и столбцов матрицы Фурье, что она может быть превращена в окаймленный циркулянт.

Этот результат принадлежит Рейдеру. Мы подробно проиллюстрируем соответствующий алгоритм в следующем пункте, посвященному БПФ длины 17, а сейчас вернемся к БПФ длины 5.

Прежде всего избавимся от единичного окаймления матрицы Фурье:

= )

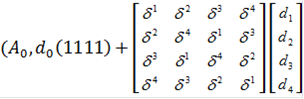
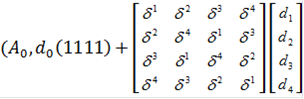В столбцах и строках матрицы, стоящей в правой части равенства выполним перестановку . Если выполним такую же перестановку координат у векторов d и его спектра А, получаем

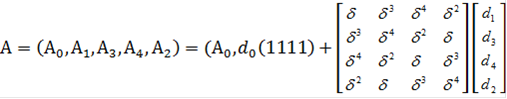
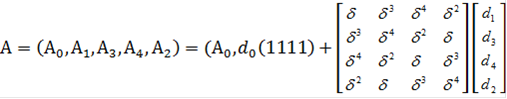) (14)